answer 8.1 - define the ligand binding polynomial
We first analyze the reaction scheme to derive how many molecules of PX, PY and PYX are in equilibrium with one molecule of the reference species P. This procedure is the same we followed in tutorial #7. The reaction scheme is:
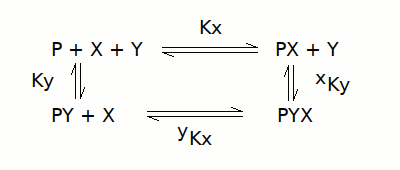
and this leads to the following set of equations:
[P] = reference species
[PX] = [P] [X] / Kx
[PY] = [P] [Y] / Ky
[PYX] = [P] [X] [Y] / yKx Ky = [P] [X] [Y] / xKy Kx
The last equation shows that yKx Ky =xKy Kx; thus only three out of four constants are independent of each other, and once three equilibrium constants are defined, the fourth follows necessarily. One can set any three at will, and if the ligand whose concentration varies over each ligand binding isotherm is X, it is sensible to set Kx, xKy, and Ky as the constants to use in the following analysis. Under these assumptions we have: yKx = Kx xKy / Ky
The binding polynomial results as follows:
[P]tot = [P] (1 + [X]/Kx + [Y]/Ky + [X][Y]/xKyKx)
The fraction of X-liganded sites, for every concentration of X and Y is:
([PX]+[PYX])/[P]tot = [X]Ky(xKy + [Y]) / [KxxKy (Ky + [Y]) + [X]Ky(xKy + [Y])]
If we equate ([PX]+[PYX])/[P]tot to 0.5 and, consequently, [X] to X50, we obtain:
X50 = Kx (KyxKy + [Y]xKy) / (KyxKy + [Y]Ky) = Kx (1 + [Y]/Ky) / (1 + [Y]/xKy)
We remark that:
| if [Y]=0 | X50 = Kx |
| if [Y]>>Ky | X50 = Kx xKy / Ky = yKx |
| if [X]=0 | [PY] / [P]tot = [Y] / (Ky + [Y]) |
| if [X]>>yKx | ([PY]+[PYX]) / [P]tot = [Y] / (xKy + [Y]) |
Proceed to next step or back one step.