Course of LABORATORY MEDICINE
Polygenic Diseases or: why are humans so different from one another?
Polygenic diseases are inherited pathological conditions that do not obey the Mendelian laws, and depend on the association of genes which are not necessarily pathological per se. Often these conditions fully develop in response of environmental stimuli and may remain silent and unnoticed for very long times.
The scope of this presentation, which is completely theorethical and does not pretend to represent any specific pathological condition or disease, is to present a very basic, and necessarily oversimplified mechanism by which non pathological gene variants (alleles) can produce pathological phenotypes.
To carry out our demonstration we shall hypothesize the following greatly simplified metabolic pathway: metabolyte A is converted by enzyme1 into metabolyte B; metabolyte B is in turn converted into waste product C by enzyme2. Waste product C is excreted:
We hypothesize that the organism is in a condition of constant metabolic flow: metabolyte A is produced at a constant rate and its concentration in the biological fluids is regulated, so that its concentration is constant. Metabolyte A is degraded in an irreversible reaction, catalyzed by enzyme1, which obeys a simple Michaelis and Menten scheme with parameters Vmax1 and Km1. Metabolyte B is potentially toxic and its accumulation is prevented by enzyme2 which degrades it irreversibly to product C in a Michaelis-type reaction scheme with Vmax2 and Km2.
The kinetic differential equations that describe our system are:
d[B]/dt = [A] Vmax1 / ([A] + Km1) - [B] Vmax2 / ([B] + Km2)
d[C]/dt = [B] Vmax2 / ([B] + Km2) - kE
A fundamental property of this system is that it is in a constant state of flow, described as a stationary state: the concentrations of A, B and C are constant, and their differential rate equations equal zero (i.e. the rate of formation equals the rate of decay). We are not interested in the concentrations of A and C, which in our model are non toxic substances; but we are interested in determinining the concentration of the potentially toxic metabolic intermediate B (suppose that B is uric acid, as in gout):
[A] Vmax1 / ([A] + Km1) = [B] Vmax2 / ([B] + Km2)
[B] = [A] Vmax1 Km2 / ([A]Vmax2 + Km1Vmax2 - [A]Vmax1)
Since we assume that [A] is precisely regulated by a variable k0 in order that its concentration is constant, it is easy to calculate the steady-state concentration of the "toxic" intermediate B. E.g. let's suppose that the concentration of A is 1 mM and that the steady state parameters of the two enzymes under physiological conditions are: Vmax1=10/s, Km1=1mM, Vmax2=10/s and Km2=1mM; we calculate:
Let's now suppose that the population presents two allelic variants of enzyme 1; these are very similar to each other, and the average values of Km and kcat of an equimolar mixture of the two variants are as reported above (a mixture of two isoenzymes does not yield perfect Michaelis hyperbolas; however if the two isoenzymes are similar to each other the deviation from the perfect hyperbola is small). Let us further suppose that each individual can be homozygous for the most active variant, heterozygous (produces 50% of the more active variant and 50% of the less active one), homozygous for the less active variant. The measurement of the enzyme activity of a blood sample from any individual may yield one of the following three Michaelis curves:
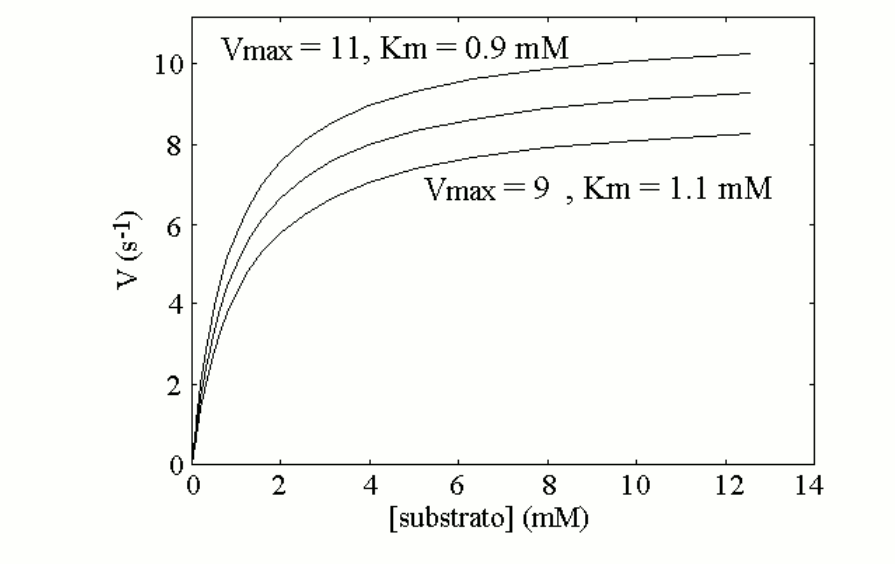
Since the two enzyme variants are both functional, and none of them qualifies as pathological, we may assume that they distribute randomly in the population and none is counterselected. If we assume that the genetic frequencies are 50% for the more active variant (E1, coded by gene E1) and 50% for the less active variant (e1, coded by gene e1), the Hardy-Weinberg law predicts the following distribution in the population: E1E1=25%; E1e1=50%; e1e1=25%. This means that 25% of the members of the population when tested will present the upper Michaelis curve, 50% the middle one and 25% the lower one.
We may now repeat the same reasoning for enzyme 2, with exactly the same numbers and we can summarize our simulation in the following table:
| Genotype | Frequency | Km1 | Vmax1 | Km2 | Vmax2 | [A] | [B] |
| E1E1-E2E2 | 6.25% | 0.900 | 11.000 | 0.900 | 11.000 | 1.000 | 1.000 |
| E1E1-E2e2 | 12.5% | 0.900 | 11.000 | 1.000 | 10.000 | 1.000 | 1.375 |
| E1E1-e2e2 | 6.25% | 0.900 | 11.000 | 1.100 | 9.000 | 1.000 | 1.984 |
| E1e1-E2E2 | 12.5% | 1.000 | 10.000 | 0.900 | 11.000 | 1.000 | 0.750 |
| E1e1-E2e2 | 25% | 1.000 | 10.000 | 1.000 | 10.000 | 1.000 | 1.000 |
| E1e1-e2e2 | 12.5% | 1.000 | 10.000 | 1.100 | 9.000 | 1.000 | 1.375 |
| e1e1-E2E2 | 6.25% | 1.100 | 9.000 | 0.900 | 11.000 | 1.000 | 0.574 |
| e1e1-E2e2 | 12.5% | 1.100 | 9.000 | 1.000 | 10.000 | 1.000 | 0.750 |
| e1e1-e2e2 | 6.25% | 1.100 | 9.000 | 1.100 | 9.000 | 1.000 | 1.000 |
| average concentration of B: 1.090 mM | |||||||
We may now group the concentration of B in classes, as observed in our population and taking into account the relative frequencies. The results are reported in the following table, together with their distribution represented as a bar diagram (each black box representing 6.25% of the population):
| [B] interval | Frequency | |||||||||
| 0.5-0.7 mM | 6.25% | |||||||||
| 0.7-0.9 mM | 25% | |||||||||
| 0.9-1.1 mM | 37.5% | |||||||||
| 1.1-1.3 mM | 0% | |||||||||
| 1.3-1.5 mM | 25% | |||||||||
| 1.5-1.7 mM | 0% | |||||||||
| 1.7-1.9 mM | 0% | |||||||||
| 1.9-2.1 mM | 6.25% | 0.5-0.7 | 0.7-0.9 | 0.9-1.1 | 1.1-1.3 | 1.3-1.5 | 1.5-1.7 | 1.7-1.9 | 1.9-2.1 |
The distribution of the serum concentration of the "toxic" metabolyte B (suppose it is urate and the disease gout) is a skewed Gaussian in which a small fraction of the population has a very low value, and a small fraction has a very high value, and actually appears as a completely distinct (pathological) group. What is most interesting is that small differences in the catalytic properties of two allelic variants of our enzymes, none of these large enough to qualify as pathological lead to large fluctuations of the steady-state concentration of the intermediate metabolyte B. Indeed we may identify in our population: a great majority of individuals having "normal" values of the metabolyte (i.e. close to the average value of 1.09 mM); a small fraction of "lucky" individuals having abnormally low values; a small fraction of "unlucky" individuals, having high values. The lucky genotype is e1e1-E2E2: these individuals are slow in producing the toxic intermediate B (they are homozygous for the low activity variant of enzyme 1) and fast in degrading it to the terminal metabolyte C. The unlicky genotype is E1E1-e2e2: these individuals produce B rapidly and degrade it slowly, with the result that it accumulates to high levels in their blood.
What this exercise of theorethical enzymology shows us is that small variations of enzyme activities, corresponding to different, non pathological allelic variants of our enzymes, may produce quite significant changes in the steady state flow of intermediate metabolytes, some of which may be associated with risk of diseases: e.g. uric acid, cholesterol, etc. A change of a factor of 2 for the concentration of a metabolyte (as the one observed above between the average value of B and that of the unlucky genotye) in our blood is usually considered large and highly significant (e.g. the fluctuations of glycemia or cholesterolemia are much lower than a factor of 2); yet the difference in the enzyme activities required for such a change may be quite small.
Home of this course