|
Andrea Bellelli Department of Biochemical Sciences "A. Rossi Fanelli", Sapienza University of Rome, Italy A scherzo presented on Thursday July 3rd, 2014 in Nove Hrady (CR), at the FEBS Avanced Course "Ligand Binding Theory and Practice" organized by Jannette Carey, Rudiger Ettrich and Wei-Feng Xue. Abstract During a discussion I made a short, unprepared comment meant to present an error which is surprisingly common in the literature, especially in enzymology, where irreversible inhibitors with non-zero values of Ki or IC50 abund. E.g. in the abstract of one paper on Thioredoxin Reductase published in J. Biol. Chem. 2005; 280: 25284-90 we read: "The IC(50) value for the enzyme was 3.6 microM after incubation at room temperature for 2 h in vitro. The inhibition occurred with enzyme only in the presence of NADPH and persisted after removal of curcumin. By using mass spectrometry and blotting analysis, we proved that this irreversible inhibition by curcumin was caused by alkylation of both residues in the catalytically active site (Cys(496)/Sec(497)) of the enzyme." I formalized that comment in this presentation whose aim is to demonstrate how apparently sound equilibrium data may nevertheless be wrong, because of insufficient control of the reaction kinetics. The experiment presented is simulated - no real data were used. Selected reference by the author Saccoccia F, Angelucci F, Boumis G, Carotti D, Desiato G, Miele AE, Bellelli A. Thioredoxin Reductase And Its Inhibitors. Curr. Protein Pept. Sci. 2014 vol. 14, pp.1-26. The experiment Suppose that you have a protein with its ligand and you are interested in measuring the equilibrium constant of the pair. After some preliminary measures, you adopt the following procedure: prepare a suitable number of samples of your protein at the lowest possible concentration (in this example we assume that your protein provides a signal at very low concentration, e.g. a change in fluorescence upon ligation); to the first you add nothing, to all others you add increasing concentrations of the ligand; you allow 5 min. to equilibrate; you record the spectra of all samples. You have varied the ligand concentration over a logarithmically spaced scale in order to cover the reaction between, say 10% and 90% saturation, and your experimental data points are as follows:
You can plot your data in the usual fractional saturation vs. ligand concentration plot, and you obtain quite a good hyperbola, as in the following figure: 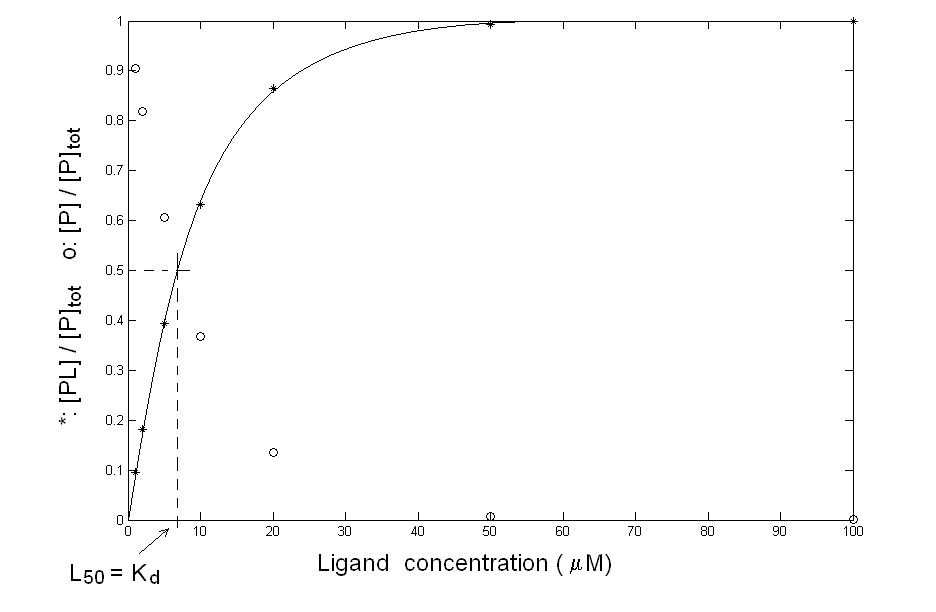
Figure 1: What you think may be the equilibrium of protein P with ligand L. Your data are compatible with the simple chemical scheme: P + L <==> PL for which the mass law dictates: Kd = [P] [L] / [PL] The above equation allows you to calculate, by means of any non linear least squares minimization routine, a Kd value of 7 μM (which equals the L50, defined as the free ligand concentration required to achieve half-saturation). Since the total protein concentration is in the nanomolar range, you are entitled to assume [L]free = [L]tot, and no corrections are required: your experimental conditions are ideal for the determination you were interested in. The control In order to further check your system, you dialyse the ligand-protein complex you have obtained, to demonstrate that the protein can be recovered unmodified after the dissociation of the ligand. Unfortun ately the complex does not dissociate upon removal of the ligand and you cannot recover the unliganded protein!. This result is completely inconsistent with the experiment you carried out since having an integer value of [PL] at [L]=0 implies irreversible binding and Kd=0. What can I do? A possible explanation of the inconsistency you found is that your experimental points were not measured under equilibrium conditions: you have allowed 5 min. to each addition of ligand but perhaps this time was not long enough for the reaction to go to completion. To check this point you should record the time courses of the reaction at selected ligand concentrations, to see how long it takes for your system to equilibrate. Your experiment yields the following result: 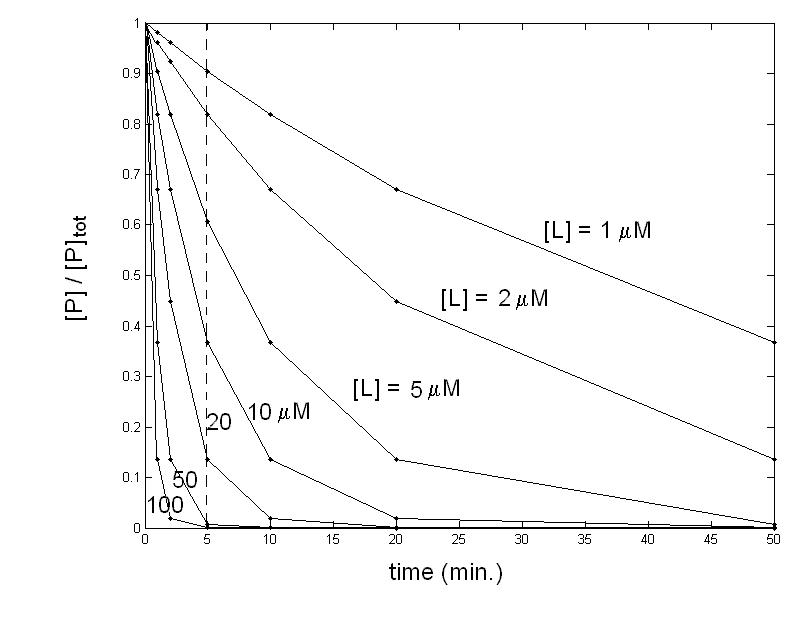
Figure 2: Time course of the decay of unliganded protein at different concentrations of the ligand. You obtained a family of pseudo first-order exponential decays. The reaction being irreversible, all your traces would end at [P]=0, if time enough had been allowed. Unfortunately all time courses in the original experiment were cut at 5 min. (dashed line). The second order kinetic rate constant of these (simulated) time courses is k=0.02 μM-1 min-1; however, given that the ligand is in large excess over the protein, its concentration may be assumed as constant within each single time course and the pseudo-first order rate constant is k'=k [L]. What happened in my "equilibrium" experiment? Now you have quite a good idea of how your system behaves, and can correctly interpret your original "equilibrium" experiment: indeed it was not at all an equilibrium experiment, it was an abortive kinetic experiment. Your system undergoes the following reaction: P + L --> PL which is irreversible and obeys (in this scherzo) a second order kinetic scheme: -d [P] / dt = k [P] [L] since [L]>>[P] you can approximate to a pseudo first order condition which integrates to: [P]t / [P]tot = e-k [L] t The above equation shows that the fration of unliganded protein depends exponentially on the incubation time, if the ligand concentration is kept constant (as observed in Fig. 2), but it also depends exponentially on the ligand concentration, if the incubation time is kept constant (as I operated to calculate the points that are plotted in Fig.1, which I erroneously fitted with a hyperbola). The L50 estimated from the data in Fig. 1 has thus the same meaning as a kinetic half-time, and equals ln 2 / kt. With the values used in this scherzo: L50 = ln 2 / kt = ln 2 / (0.02 x 5) = 6.93 μM Obviously the L50 is never defined as a kinetic parameter and should never used as above; what we should say is that the t1/2 of the irreversible combination reaction is 5 min. when measured at a ligand concentration of 6.93 μM. In practice you would not work exactly as I described in this scherzo: most often you would record your equilibrium curve using only one protein sample and adding successive aliquots of the ligand. In this case the ligand added in the first step continues to react while you record the successive steps and this scrambles the correspondence between the putative equilibrium and its kinetic explanation. However, something can be learned even from a purely theoretical scherzo like this one: 1) Control experiments (in this case the the reversibilty check by dialysis) are important. 2) It is always a good idea to check the kinetics of your reaction, even when you are only interested in its equilibrium parameters. 3) To measure an equilibrium constant each of the experimental points must have reached the equilibrium condition (this takes at least 4-5 half times of the reaction). 4) An exponential and a hyperbola are not so different, and both are observed in chemistry: the former in kinetics, the latter in equilibria! This makes errors like the one described above not only possible but quite common. Home page |