|
Andrea Bellelli Department of Biochemical Sciences "A. Rossi Fanelli", Sapienza University of Rome, Italy Lecture presented in Nove Hrady (CR), at the 2016 FEBS Avanced Course "Ligand Binding Theory and Practice" organized by Jannette Carey, Rudiger Ettrich and Wei-Feng Xue. Abstract UV/Vis absorbance spectroscopy is a powerful tool to detect the binding of a ligand to a protein; however it may be abused, leading to wrong determinations. In this lecture the following topics wil be considered: (i) the nature of absorbance changes and their (putative) relationship to ligand binding (ii) the problem of "linearity" of the signal or lack thereof (iii) the single wavelength analysis according to the law of Lambert and Beer (iv) a matrix approach to multiple wavelength analysis. Some real examples are presented, but most of the analysis will be carried out on simulated data. Selected reference by the author Bellelli A, Brunori M. (1994) Optical measurements of quaternary structural changes in hemoglobin. Methods Enzymol.; 232: 56-71. Antonini G, Bellelli A, Brunori M, Falcioni G. (1996) Kinetic and spectroscopic properties of the cyanide complexes of ferrous haemoglobins I and IV from trout blood. Biochem J.;314: 533-540. Nature of UV/Vis absorbance changes UV/Vis photons have energy enough to cause quantum transitions in the electrons present in bonding orbitals: e.g. pi to pi* quantum jumps. If the binding of a ligand to a protein occurs via formation of a true chemical bond, it is directly associated to a change of the absorbance spectrum (with respect to the free, unbound couple of the protein and the ligand). Given the energies of photons in the near UV/Vis wavelength range, absorption is essentially confined to the quantum transitions of delocalized pi electrons of aromatic chromophores (i.e. aromatic residues or co-factors). Unfortunately only a handful of protein ligands form bonding orbitals with their characteristic absorbance spectra. In many cases the protein-ligand complex forms because of weak chemical interactions (H-bonds, hydrophobic contacts, etc.) that are spectroscopically silent; even in these cases, however, the presence of the ligand in the binding site may perturb the absorbance spectra of some protein chromophore (e.g. a Trp residue in the binding site), and be associated to a detectable UV/Vis absorbance change. The experimental measurement of absorbance is carried out using UV/Vis spectrophotometers, i.e. instruments in which a suitable light source illuminates the sample and a detector measures the amount of light which is transmitted through the sample: 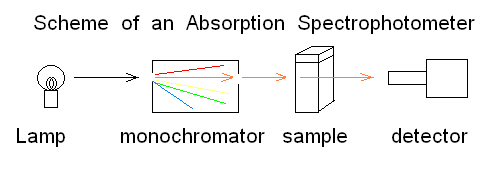
Fig.1: Simplified scheme of an absorbance spectrophotometer To carry out a measurement using the simplest instrument schematized in the above Fig.1, the researcher puts in the sample compartment a spectrophotometric cuvette containing the "blank" (i.e. the buffer he will use during actual the measurements) and records the light energy transmitted at the appropriate wavelength. He then replaces the blank with the sample and takes a new reading. The following definitions apply:
In order to correct for lamp intensity oscillations, most research spectrophotometers adopt a double beam design in which a sample and a matched blank are read alternatively; moreover, a motorized monochromator allows the researcher to record the full absorbance spectrum of his/her sample, i.e. to scan the absorbance over an arbitrarily defined range of wavelengths. 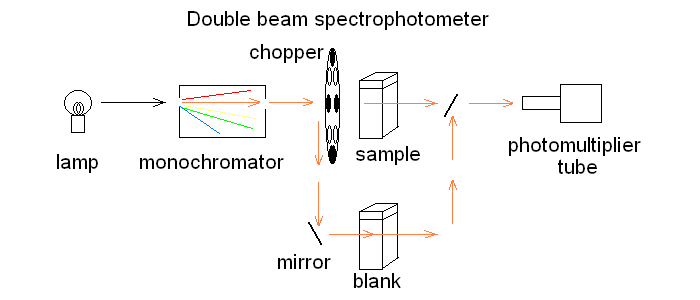 UV/Vis absorption is governed by the law discovered by Lambert and Beer: Lambert's law essentially states that Absorbance is directly proportional (= linearly correlated) to concentration, i.e. that the measure of the former allows the researcher to calculate the latter, not a small feat for complex biological macromolecules that do not lend themselves to easy direct chemical determinations. Application of absorbance measurements to ligand binding equilibria (and kinetics). If we record absorbance spectra of the same protein solution equilibrated with different concentrations of its ligand X, and if formation of the complex is associated to an absorbance change, we obtain a series of spectra, whose absorbance values are linear combinations of those of the ligand, the unliganded protein and the protein-ligand complex: Most often the extinction coefficient of the ligand is negligible, thus the free ligand concentration can be neglected in the Asorbance expression. Moreover, the terms [P] and [PL] sum to the total protein concentration [P]tot, and can be expressed as a function of the fractional ligand saturation Y, defined as Y = [PL] / [P]tot; thus we obtain A classical example of the application of absorbance spectroscopy to the study of ligand binding is provided by hemoproteins, which form a coordination complex with their ligands using the iron atom of their heme group. The heme has an extended aromatic ring which presents at least two π -> π* electronic transitions, one excited by light in the wavelength range 450-400 nm (the Soret or γ band) and one excited by light in the visible range (the α band). A second absorbance band in the same range may result from the vibronic mixing of the former two (the β band). The relative amplitudes and positions of the α, β, and γ bands depends on the presence or absence of the ligand, and on its nature, as well as on the symmetry of the complex: thus the absorbance spectra of unliganded and liganded hemoproteins differ, as shown in the experiment of reversible binding of n-propyl isocyanide to ferrous Hb reported below. 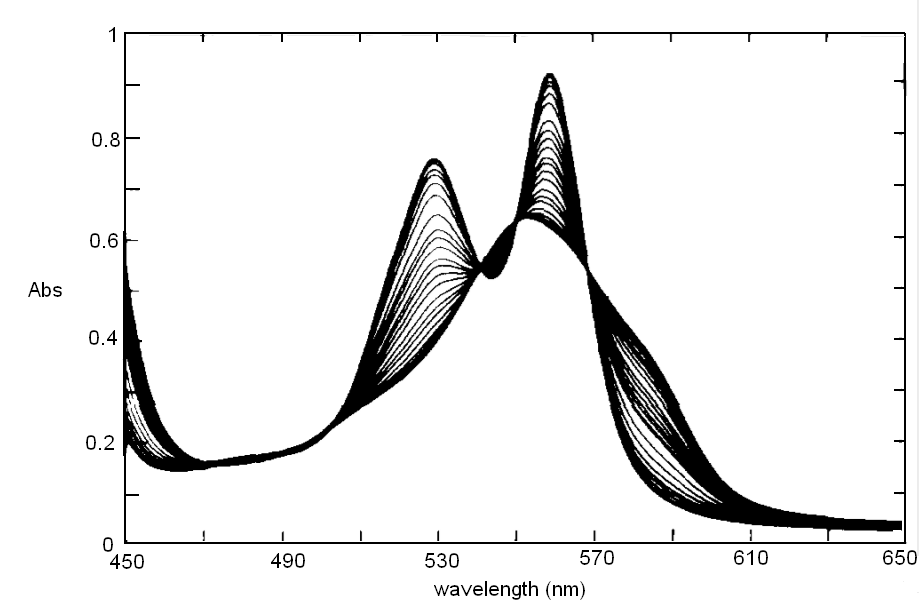
Fig. 3: Reversible binding of n-propyl isocyanide to human hemoglobin, monitored by absorbance spectroscopy (modified after Reisberg and Olson, J. Biol. Chem. 1980, 255, 4144-4150) Linearity Absorbance spectroscopy, thanks to Lambert's law is so powerful and so useful a technique for the study of ligand binding that its limitations and difficulties are often overlooked. The most important problem with absorbance spectroscopy is to make sure that the absorbance signal is indeed linear with binding. One should not confuse the linear relationship of absorbance to concentration (Lambert's law) with linearity to binding: indeed the absorbance change may be due to a ligand-dependent structural rearrangement of the protein, and the relationship between the two phenomena of ligation and structural change may be non-linear. Linearity should be tested by experiment, under conditions in which the fraction of liganded sites Y is known independently. E.g. E. Antonini and S. Anderson demonstrated the linearity of absorbance changes and ligand binding in HbCO, taking advantage of the high affinity of the ligand, whose free concentration, under suitable experimental conditions is negligible. 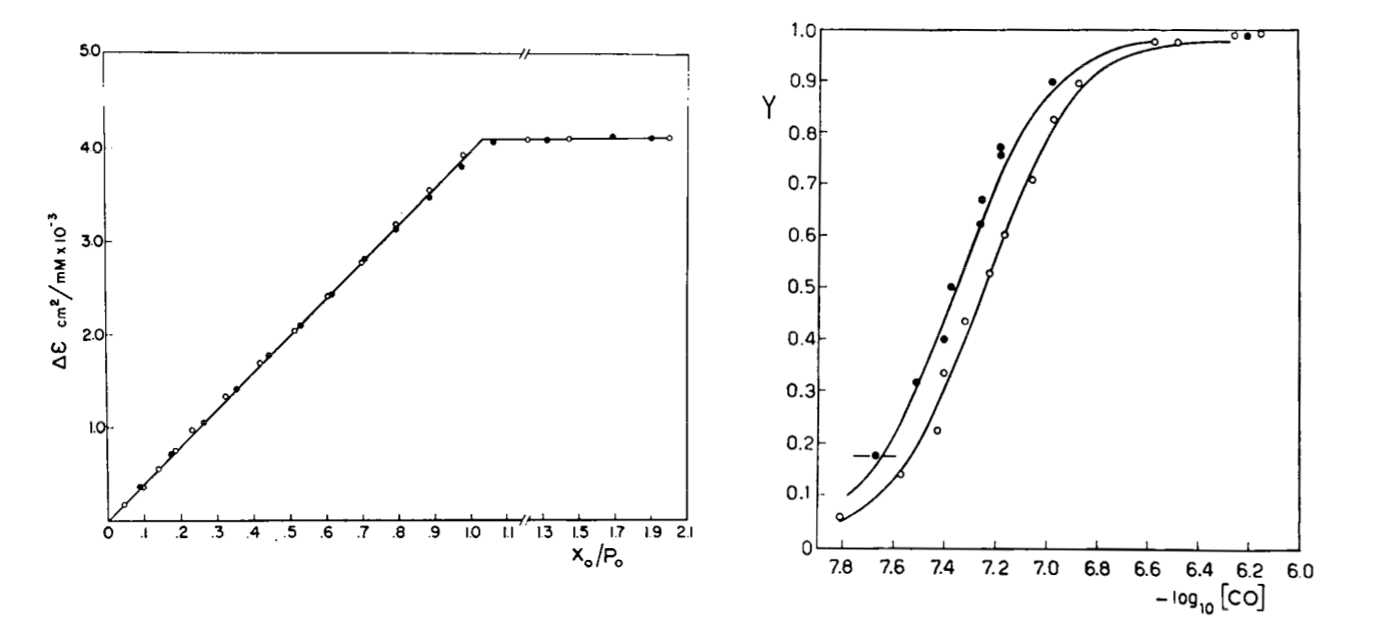 By contrast, Imai and Yonetani studied a spectroscopic feature of the same reaction in the near UV region, which they attributed to the solvent exposure of a Trp residue as a consequence of ligand-linked structure changes of the protein, and demonstrated it to be non-linear to ligand saturation. 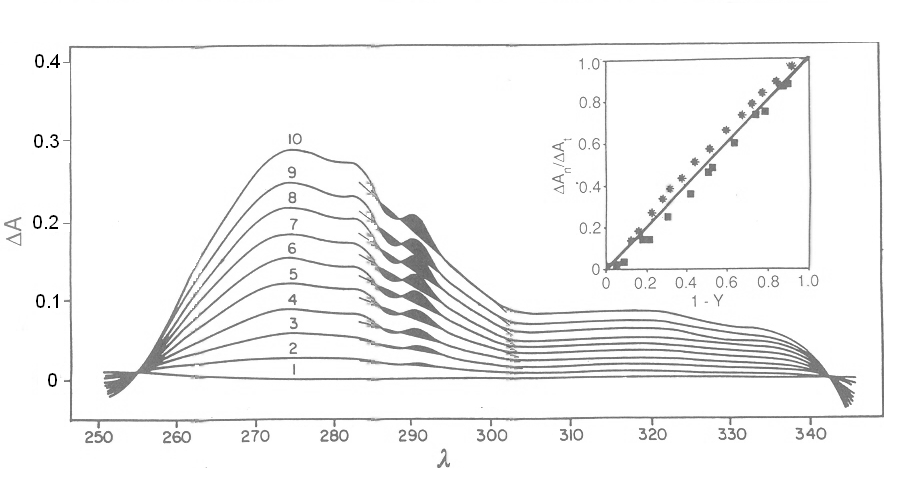
Fig. 4: Ligand-dependent spectroscopic changes in the UV absorbance spectrum of hemoglobin (see text) Explanation of non-linearity Lambert's law guarantees that absorbance is linearly related to concentration, but in an oligomeric protein an absorbance change may be linearly related to a structural change, which is induced by the ligand but not linearly related to ligand saturation. The most straighforward case is that of an allosteric protein, like hemoglobin, which is stable in two structural conformations. The classical allosteric model of Monod, Wyman and Changeux (1965) postulates that the two structural conformations, called R and T, are in equilibrium irrespective of the presence of the ligand, and their relative population is biased by ligation. The energy diagram of the model is as follows: 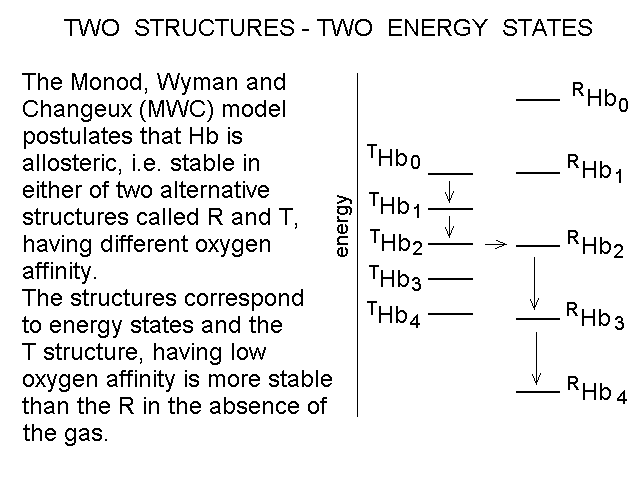 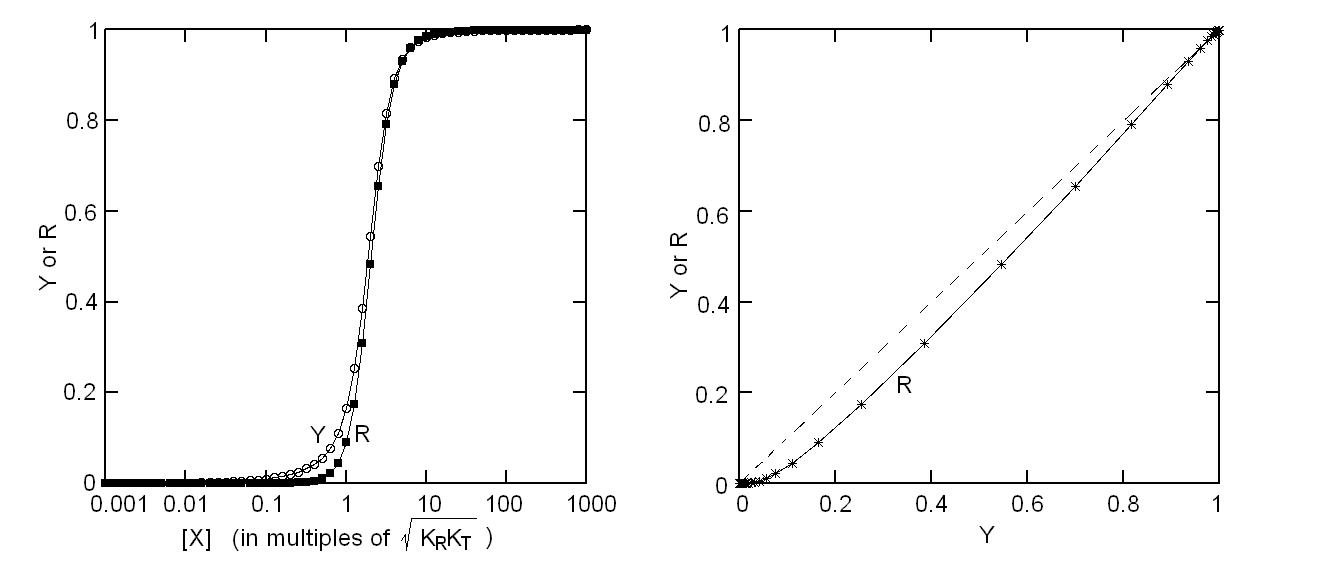
Fig. 5: Relationship between population of the high affinity state of an allosteric tetramer and ligand saturation (see text) Isosbestic points Isosbestic points are wavelengths at which the extinction coefficients of the liganded and unliganded (or any couple of) derivatives have the same extinction coefficients. If the chemical reaction one is studying only involves two chemical species (i.e. the reactant and the product), one finds perfect isosbestic points (see Fig. 3). Isosbestic points do not guarantee linearity of the absorbance signal to binding, nor does lack of them demonstrate absence of linearity; however lack of isosbestic points demonstrates that the reaction has at least three species (e.g. reactant, intermediate and product) and implies that the absorbance signal is non-linear to binding at least at some wavelengths. Important cases of lack of linearity in the presence of isosbestic points occur when the reaction we study has intermediates which can be spectroscopically resolved only in limited regions of the spectrum (e.g. the UV feature identified by Imai and Yonetani in the UV spectrum of Hb occurs in a region which has isosbestic points at 255 and 343 nm). Multiple components analysis If the reaction of interest involves multiple spectroscopically distinct intermediates, its analysis is usually complex and model-dependent. The essential features of this system are: (i) signal may not be linear with ligation; and (ii) the spectroscopic transition may lack true isosbestic points. Matrices are a powerful instrument to deal with these conditions, since matrix operations allow the researcher to analyze full spectra at once, rathre than single wavelengths. If we collect the spectra of our experiment in a matrix A in which each column is a spectrum and each row a time course or equilibrium profile at a single wavelength, we can express Lambert's law as the product of matrices ε (the matrix of the extinction coefficients of the relevant chemical species) and C (the matrix of the concentrations of the relevant chemical species): 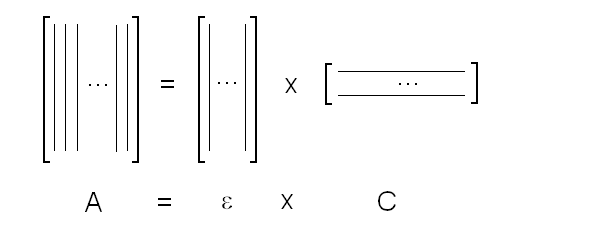 The main limit of this approach is that we must provide the matrix of extinction coefficients for all the intermediate species involved, and some of these may not be available (e.g. some ligation intermediates cannot be prepared in a purified state). Matrix algebra offers an elegant solution to this problem, called the Singular Value Decomposition (SVD). SVD decomposes matrix A into the product of three matrices, called U, S, and V, such that: The SVD solution is unique because of the following internal constraints: (i) U and V are orthogonal matrices, i.e. their transpose is also their inverse; (ii) S is a diagonal matrix whose nonzero elements are positive and arrenged in decreasing order. If the dimensions of A are mxn (i.e. n spectra of m wavelength readings have been collected), the dimensions of U are mxn, those of S and V are nxn. The mxn UxS matrix is formally analogous a matrix of extinction coefficients ε, and given the decreasing order of the elements of S, only the first few columns are significant, the remaining ones containing mostly noise. The columns of matrix V contain the ligand-dependent amplitudes of the spectroscopic components UxS, i.e. they are analogous to the concentrations of the chemical species. Home page |