| |
A CHEMISTRY-INSPIRED MODEL OF EPIDEMICS
Andrea Bellelli and Francesco Malatesta
UNIVERSITA' DI ROMA SAPIENZA
FACOLTA' DI FARMACIA E MEDICINA
The medical student may be familiar with chemical kinetics, as studied in courses of Chemistry and Biochemistry; moreover, he or she will have applied the concepts of chemical kinetics to pharmacodynamics during his/her course of Pharmacology. Chemical kinetics is essentially an application of elementary statistical principles, and may be a source of inspiration for several statistical phenomena. In the present exercise we derive a model of epidemics based on the same statistical laws that govern chemical kinetics. This exercise is not meant to be a research instrument: its purpose is pedagogical, and serves to illustrate some concepts like the R0, herd immunity and attack rate, whose statistical and mechanistical bases may require more than a qualitative explanation. An epidemic is conceptually similar to a proteolytic cascade in which the zymogen is the substrate of the enzyme, e.g. the trypsin-catalyzed conversion of trypsinogen to trypsin. In order to make this analogy more stringent, we need to postulate two more steps, describing respectively a structural rearrangement of the enzyme, required for its activity, and an inactivation step. Thus, the kinetic model is as follows:
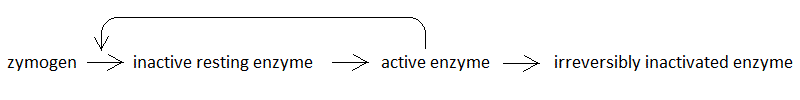The first reaction is second order and requires the collision of the zymogen with the active enzyme; all other reactions are first order. The student will immediately recognize the similarity to a standard epidemic model in which each member of the population may assume one among four possible states: Susceptible (S); Infected, non contagious (I1); Infected and contagious (I2); Recovered (R). These states are arranged as a series of irreversible transformations:
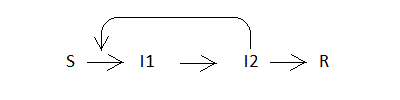The transformation of S to I1 (infection) requires contact with I2, whereas the following steps describe the course of the disease and do not require interpersonal contacts. The conversion of I1 to I2 describes the incubation period of the disease, that from I2 to R its clinical course. The patient is assumed to be contagious only if in state I2. We recognize that molecular epidemics and population epidemics differ under many respects, e.g. encounters between molecules and encounters between persons are governed by different statistical laws and even the concepts of molecular concentration and population density do not match; thus our analogy is only approximate and qualitative. The model here presented is a variant of the one developed by Kermack and Mc Kendrick in 1927 (see A contribution to the mathematical theory of epidemics; see also Kermack-McKendrick Model; Il modello di Kermack e McKendrick per la peste a Bombay e la riproducibilità di un tipo con stagionalita'). With respect to the riginal formulation we split the infected state into two substates (I1 and I2) in order to describe the incubation period and to improve the simulation of the course of the disease.
You can simulate your own epidemic! Just fill in the parameters you want to explore in the table below and press the [send] button. The constants are expressed as the reciprocal of time units (days-1).
|
|